I’m at Princeton where Ed Snowden is due to speak by live video link in a few minutes, and have a discussion with Bart Gellmann.
Yesterday he spent four hours with a group of cryptographers from industry and academia, of which I was privileged to be one. The topic was the possible and likely countermeasures, both legal and technical, against state surveillance. Ed attended as the “Snobot”, a telepresence robot that let him speak to us, listen and move round the room, from a studio in Moscow. As well as over a dozen cryptographers there was at least one lawyer and at least one journalist familiar with the leaked documents. Yesterday’s meeting was under the Chatham House rule, so I may not say who said what; any new disclosures may have been made by Snowden, or by one of the journalists, or by one of the cryptographers who has assisted journalists with the material. Although most of what was discussed has probably appeared already in one place or another, as a matter of prudence I’m publishing these notes on the blog while I’m enjoying US first-amendment rights, and will sanitise them from my laptop before coming back through UK customs.
The problem of state surveillance is a global one rather than an NSA issue, and has been growing for years, along with public awareness of it. But we learned a lot from the leaks; for example, wiretaps on the communications between data centres were something nobody thought of; and it might do no harm to think a bit more about the backhaul in CDNs. (A website that runs TLS to a CDN and then bareback to the main server is actually worse than nothing, as we lose the ability to shame them.) Of course the agencies will go for the low-hanging fruit. Second, we also got some reassurance; for example, TLS works, unless the agencies have managed to steal or coerce the private keys, or hack the end systems. (This is a complex discussion given CDNs, problems with the CA ecology and bugs like Heartbleed.) And it’s a matter of record that Ed trusted his life to Tor, because he saw from the other side that it worked.
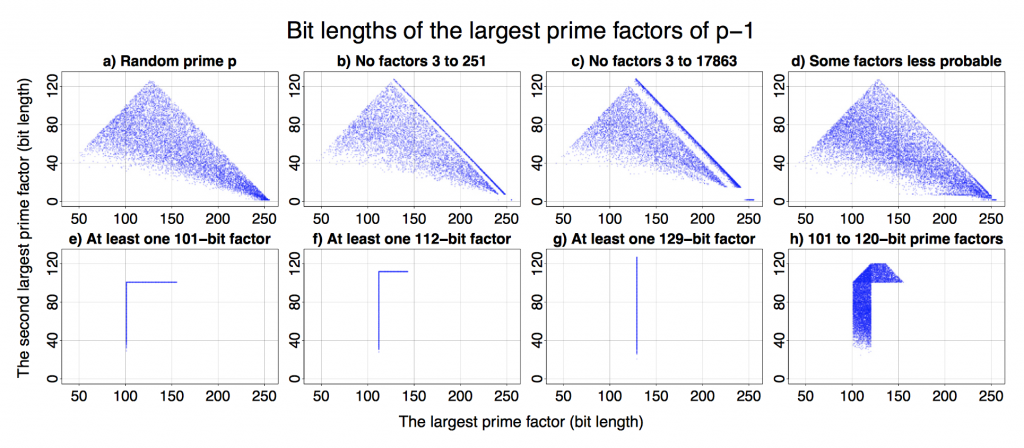
Third, the leaks give us a clear view of an intelligence analyst’s workflow. She will mainly look in Xkeyscore which is the Google of 5eyes comint; it’s a federated system hoovering up masses of stuff not just from 5eyes own assets but from other countries where the NSA cooperates or pays for access. Data are “ingested” into a vast rolling buffer; an analyst can run a federated search, using a selector (such as an IP address) or fingerprint (something that can be matched against the traffic). There are other such systems: “Dancing oasis” is the middle eastern version. Some xkeyscore assets are actually compromised third-party systems; there are multiple cases of rooted SMS servers that are queried in place and the results exfiltrated. Others involve vast infrastructure, like Tempora. If data in Xkeyscore are marked as of interest, they’re moved to Pinwale to be memorialised for 5+ years. This is one function of the MDRs (massive data repositories, now more tactfully renamed mission data repositories) like Utah. At present storage is behind ingestion. Xkeyscore buffer times just depend on volumes and what storage they managed to install, plus what they manage to filter out.
As for crypto capabilities, a lot of stuff is decrypted automatically on ingest (e.g. using a “stolen cert”, presumably a private key obtained through hacking). Else the analyst sends the ciphertext to CES and they either decrypt it or say they can’t. There’s no evidence of a “wow” cryptanalysis; it was key theft, or an implant, or a predicted RNG or supply-chain interference. Cryptanalysis has been seen of RC4, but not of elliptic curve crypto, and there’s no sign of exploits against other commonly used algorithms. Of course, the vendors of some products have been coopted, notably skype. Homegrown crypto is routinely problematic, but properly implemented crypto keeps the agency out; gpg ciphertexts with RSA 1024 were returned as fails.
With IKE the NSA were interested in getting the original handshakes, harvesting them all systematically worldwide. These are databased and indexed. The quantum type attacks were common against non-crypto traffic; it’s easy to spam a poisoned link. However there is no evidence at all of active attacks on cryptographic protocols, or of any break-and-poison attack on crypto links. It is however possible that the hacking crew can use your cryptography to go after your end system rather than the content, if for example your crypto software has a buffer overflow.
What else might we learn from the disclosures when designing and implementing crypto? Well, read the disclosures and use your brain. Why did GCHQ bother stealing all the SIM card keys for Iceland from Gemalto, unless they have access to the local GSM radio links? Just look at the roof panels on US or UK embassies, that look like concrete but are actually transparent to RF. So when designing a protocol ask yourself whether a local listener is a serious consideration.
In addition to the Gemalto case, Belgacom is another case of hacking X to get at Y. The kind of attack here is now completely routine: you look for the HR spreadsheet in corporate email traffic, use this to identify the sysadmins, then chain your way in. Companies need to have some clue if they’re to stop attacks like this succeeding almost trivially. By routinely hacking companies of interest, the agencies are comprehensively undermining the security of critical infrastructure, and claim it’s a “nobody but us” capability. however that’s not going to last; other countries will catch up.
Would opportunistic encryption help, such as using unauthenticated Diffie-Hellman everwhere? Quite probably; but governments might then simply compel the big service forms to make the seeds predictable. At present, key theft is probably more common than key compulsion in US operations (though other countries may be different). If the US government ever does use compelled certs, it’s more likely to be the FBI than the NSA, because of the latter’s focus on foreign targets. The FBI will occasionally buy hacked servers to run in place as honeypots, but Stuxnet and Flame used stolen certs. Bear in mind that anyone outside the USA has zero rights under US law.
Is it sensible to use medium-security systems such as Skype to hide traffic, even though they will give law enforcement access? For example, an NGO contacting people in one of the Stans might not want to incriminate them by using cryptography. The problem with this is that systems like Skype will give access not just to the FBI but to all sorts of really unsavoury police forces.
FBI operations can be opaque because of the care they take with parallel construction; the Lavabit case was maybe an example. It could have been easy to steal the key, but then how would the intercepted content have been used in court? In practice, there are tons of convictions made on the basis of cargo manifests, travel plans, calendars and other such plaintext data about which a suitable story can be told. The FBI considers it to be good practice to just grab all traffic data and memorialise it forever.
The NSA is even more cautious than the FBI, and won’t use top exploits against clueful targets unless it really matters. Intelligence services are at least aware of the risk of losing a capability, unlike vanilla law enforcement, who once they have a tool will use it against absolutely everybody.
Using network intrusion detection against bad actors is very much like the attack / defence evolution seen in the anti-virus business. A system called Tutelage uses Xkeyscore infrastructure and matches network traffic against signatures, just like AV, but it has the same weaknesses. Script kiddies are easily identifiable from their script signatures via Xkeyscore, but the real bad actors know how to change network signatures, just as modern malware uses packers to become highly polymorphic.
Cooperation with companies on network intrusion detection is tied up with liability games. DDoS attacks from Iran spooked US banks, which invited the government in to snoop on their networks, but above all wanted liability protection.
Usability is critical. Lots of good crypto never got widely adopted as it was too hard to use; think of PGP. On the other hand, Tails is horrifically vulnerable to traditional endpoint attacks, but you can give it as a package to journalists to use so they won’t make so many mistakes. The source has to think “How can I protect myself?” which makes it really hard, especially for a source without a crypto and security background. You just can’t trust random journalists to be clueful about everything from scripting to airgaps. Come to think of it, a naive source shouldn’t trust their life to securedrop; he should use gpg before he sends stuff to it but he won’t figure out that it’s a good idea to suppress key IDs. Engineers who design stuff for whistleblowers and journalists must be really thoughtful and careful if they want to ensure their users won’t die when they screw up. The goal should be that no single error should be fatal, and so long as their failures aren’t compounded the users will stay alive. Bear in mind that non-roman-language countries use numeric passwords, and often just 8 digits. And being a target can really change the way you operate. For example, password managers are great, but not for someone like Ed, as they put too many of the eggs in one basket. If you’re a target, create a memory castle, or a token that can be destroyed on short notice. If you’re a target like Ed, you have to compartmentalise.
On the policy front, one of the eye-openers was the scale of intelligence sharing – it’s not just 5 eyes, but 15 or 35 or even 65 once you count all the countries sharing stuff with the NSA. So how does governance work? Quite simply, the NSA doesn’t care about policy. Their OGC has 100 lawyers whose job is to “enable the mission”; to figure out loopholes or new interpretations of the law that let stuff get done. How do you restrain this? Could you use courts in other countries, that have stronger human-rights law? The precedents are not encouraging. New Zealand’s GCSB was sharing intel with Bangladesh agencies while the NZ government was investigating them for human-rights abuses. Ramstein in Germany is involved in all the drone killings, as fibre is needed to keep latency down low enough for remote vehicle pilots. The problem is that the intelligence agencies figure out ways to shield the authorities from culpability, and this should not happen.
Jurisdiction is a big soft spot. When will CDNs get tapped on the shoulder by local law enforcement in dodgy countries? Can you lock stuff out of particular jurisdictions, so your stuff doesn’t end up in Egypt just for load-balancing reasons? Can the NSA force data to be rehomed in a friendly jurisdiction, e.g. by a light DoS? Then they “request” stuff from a partner rather than “collecting” it.
The spooks’ lawyers play games saying for example that they dumped content, but if you know IP address and file size you often have it; and IP address is a good enough pseudonym for most intel / LE use. They deny that they outsource to do legal arbitrage (e.g. NSA spies on Brits and GCHQ returns the favour by spying on Americans). Are they telling the truth? In theory there will be an MOU between NSA and the partner agency stipulating respect for each others’ laws, but there can be caveats, such as a classified version which says “this is not a binding legal document”. The sad fact is that law and legislators are losing the capability to hold people in the intelligence world to account, and also losing the appetite for it.
The deepest problem is that the system architecture that has evolved in recent years holds masses of information on many people with no intelligence value, but with vast potential for political abuse.
Traditional law enforcement worked on individualised suspicion; end-system compromise is better than mass search. Ed is on the record as leaving to the journalists all decisions about what targeted attacks to talk about, as many of them are against real bad people, and as a matter of principle we don’t want to stop targeted attacks.
Interference with crypto in academia and industry is longstanding. People who intern with a clearance get a “lifetime obligation” when they go through indoctrination (yes, that’s what it’s called), and this includes pre-publication review of anything relevant they write. The prepublication review board (PRB) at the CIA is notoriously unresponsive and you have to litigate to write a book. There are also specific programmes to recruit cryptographers, with a view to having friendly insiders in companies that might use or deploy crypto.
The export control mechanisms are also used as an early warning mechanism, to tip off the agency that kit X will be shipped to country Y on date Z. Then the technicians can insert an implant without anyone at the exporting company knowing a thing. This is usually much better than getting stuff Trojanned by the vendor.
Western governments are foolish to think they can develop NOBUS (no-one but us) technology and press the stop button when things go wrong, as this might not be true for ever. Stuxnet was highly targeted and carefully delivered but it ended up in Indonesia too. Developing countries talk of our first-mover advantage in carbon industrialisation, and push back when we ask them to burn less coal. They will make the same security arguments as our governments and use the same techniques, but without the same standards of care. Bear in mind, on the equities issue, that attack is way way easier than defence. So is cyber-war plausible? Politically no, but at the expert level it might eventually be so. Eventually something scary will happen, and then infrastructure companies will care more, but it’s doubtful that anyone will do a sufficiently coordinated attack on enough diverse plant through different firewalls and so on to pose a major threat to life.
How can we push back on the poisoning of the crypto/security community? We have to accept that some people are pro-NSA while others are pro-humanity. Some researchers do responsible disclosure while others devise zero-days and sell them to the NSA or Vupen. We can push back a bit by blocking papers from conferences or otherwise denying academic credit where researchers prefer cash or patriotism to responsible disclosure, but that only goes so far. People who can pay for a new kitchen with their first exploit sale can get very patriotic; NSA contractors have a higher standard of living than academics. It’s best to develop a culture where people with and without clearances agree that crypto must be open and robust. The FREAK attack was based on export crypto of the 1990s.
We must also strengthen post-national norms in academia, while in the software world we need transparency, not just in the sense of open source but of business relationships too. Open source makes it harder for security companies to sell different versions of the product to people we like and people we hate. And the NSA may have thought dual-EC was OK because they were so close to RSA; a sceptical purchaser should have observed how many government speakers help them out at the RSA conference!
Secret laws are pure poison; government lawyers claim authority and act on it, and we don’t know about it. Transparency about what governments can and can’t do is vital.
On the technical front, we can’t replace the existing infrastructure, so it won’t be possible in the short term to give people mobile phones that can’t be tracked. However it is possible to layer new communications systems on top of what already exists, as with the new generation of messaging apps that support end-to-end crypto with no key escrow. As for whether such systems take off on a large enough scale to make a difference, ultimately it will all be about incentives.